ごきげんよう、二深すうちです。
私は今、「データを扱える人」になりたく「統計学を勉強してみよう」と本企画を立てました。
(※現在の私の立場は開発現場のPMO(一部PM)の人です。)
本企画は「統計学が最強の学問である」を読んで、自分なりに解釈・噛み砕いてアウトプットする企画です。
本記事は「統計学が最強の学問である」の第三章を二深すうちワールドでお話ししていきたいと思います。
統計学のキモは誤差と因果関係である
「統計学が最強の学問である」の第三章では、統計学のキモは誤差と因果関係ということを説明してくれるようです。ひたすら数字に騙されるな。の類を説明してくれます。
データをビジネスに使うための3つの問い
世の中には、データの集計を解析結果として提示されたグラフがしばしばあるそうです。
そのグラフを見ても、せいぜい現状把握ができるくらいで、次に何をすればいいのか分からず、「ふーん」と言うしかないのです。
「データ分析において重要なのは、”果たしてその解析はかけたコスト以上の利益を自社にもたらすような判断に繋がるのだろうか”という視点が必要だ」と著者は言います。
そして、そうした具体的な行動を引き出すためには、少なくとも3つの問いに答えられないといけないようです。
問1:何かの要因が変化すれば利益は向上するのか
問2:そうした変化を起こすような行動は実際に可能なのか
問3:変化を起こす行動が可能だとしてその利益はコストを上回るのか
この3つの問いに答えられた時、はじめて”行動を起こすことで利益を向上させる”という見通しが立つのであり、そうでなければ、わざわざ統計解析に従って新たなアクションを取ろうとする意味はない。とのこと。
例えば、「現在の当社のブランドについてのグラフ」を作ったとする。
結果として、大変好ましい38%・好ましい18%・どちらともいえない9%・好ましくない11%・大変好ましくない24%で分かれた集計となる。
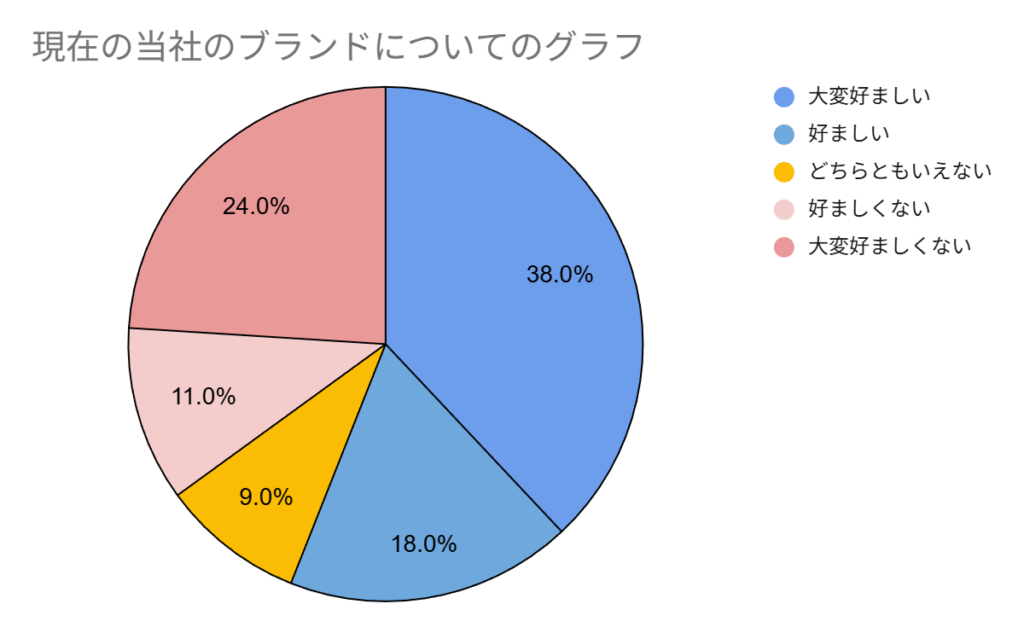
さて、これで何が分かるというのでしょう。
「おお、半数以上の人(大変好ましい38%・好ましい18%計=56%)が好ましいと思ってくれるんだね~とは言っても、好ましいと思っていない人も(好ましくない11%・大変好ましくない24%計=35%)それなりにいるね~」くらいですかね。
本当に欲しい内容としては、「好感度が高い人ほど購買金額が多いのか?」という点や「では実際に何かの行動によって好感度を上げることができるのだろうか」という点、「そのためにどれくらいのコストをかければどれだけの利益に繋がるのだろう」という点が必要なわけです。これでは現状を知れたに過ぎず、今後どうしていくべきかという方向性は何も分かりません。(問1・2・3に答えられていない)
さらに例えば、当社の顧客データから性別・年齢ごとの平均売り上げ単価のグラフを作ったとする。
これでできるとしたら、比較的単価の高い世代の顧客層を狙ったキャンペーンを打つことぐらいで、「問2:そうした変化を起こすような行動は実際に可能なのか」や「問3:変化を起こす行動が可能だとしてその利益はコストを上回るのか」には答えられません。
この、”平均”や”パーセンテージ”を計算するような古典的な統計は19世紀初頭から世界各国で取られていて、有名どころでナイチンゲールの偉業の一つに「戦争に従軍した兵士の死因を集計した結果、戦闘で負った傷自体で亡くなる兵士よりも、負傷後に何かしらの菌に感染したせいで死亡する兵士の方が圧倒的に多いことを明らかにした」ことがあります。
このことにより、一章でお話ししたような、「悪いか良いかは一旦どうでもいい。とにかくやめろ。とにかく下げろ」という、最速で最善の答えを出す統計学的なアプローチで、「戦争で兵士や国民の命を失いたくなければ、清潔な病院を戦場に整備しろ」と迫ったそうです。
ナイチンゲールの統計は、「何が起きているのか」を明らかにすることは成功しました。
しかし、このナイチンゲールの統計も「本当に清潔な病院を整備すれば戦死者を減らせるのか」、「病院の整備にどれだけのコストをかければ命が救われるのか」といった点は答えられていないのです。
そう、19世紀の統計学から100年経った20世紀は、現代的な統計学の手法も使わなければならなくなったのです。
この世は因果関係を考えない統計分析で溢れている
皆さんは普段グラフというものを見ますか?
そしてそのグラフはどれくらい価値のあるモノでしょうか。
ちなみに私が直近で見たグラフは転職サイトの年代別転職率です。
正直、だからどうしたの?とは思いましたが。
例えば、プロモーションキャンペーンの評価レポートとしてグラフを提示しました。
「あなたは過去1カ月の間に当社の○○キャンペーンの報告を見たことがありますか」というような集計で、
「見た8%・多分見た38%・分からない41%・見てない13%」で分かれています。
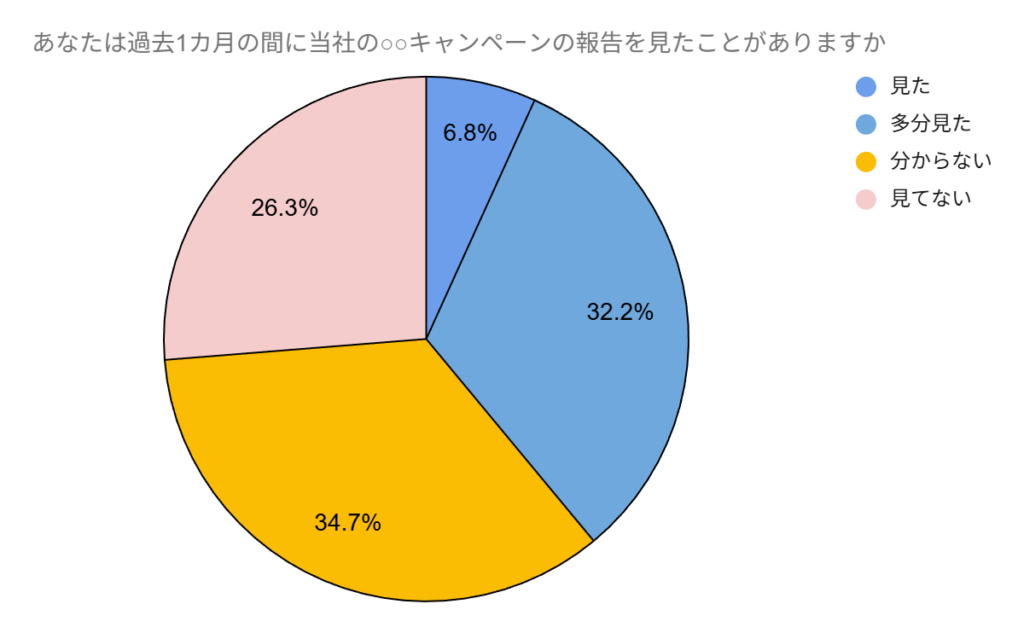
この結果として、「見た8%・多分見た38%」を合わせて46%、約半数の高い認知率を獲得しました。キャンペーンは成功です!というものです。
さて実はこのデータの出所は、キャンペーンの対象とした商品購入後のアンケートだったのです。
そりゃあ・・・一般よりも見やすい可能性高いでしょ・・・。
このような偏りの大きいデータから示したキャンペーンの認識率が大きいからと言って、いったい何だというのだろうか。と著者は言います。それは、そう。。。
ちなみに、仮にキャンペーンの認知率を日本全体のランダムサンプルから正確に測定できたとしてもだから何?という話の域を出ない。実際に購買というアクションに繋がらなければ何の意味も持たないのである。とも著者は言います。
先ほどの私の体験談である転職サイトの年代別転職率も確かに、だからどうしたの?って思ってしまった。。。
これがさらに例えば、非商品購入者へのアンケートで「見た19%・多分見た49%・分からない25%・見てない7%」と出た場合
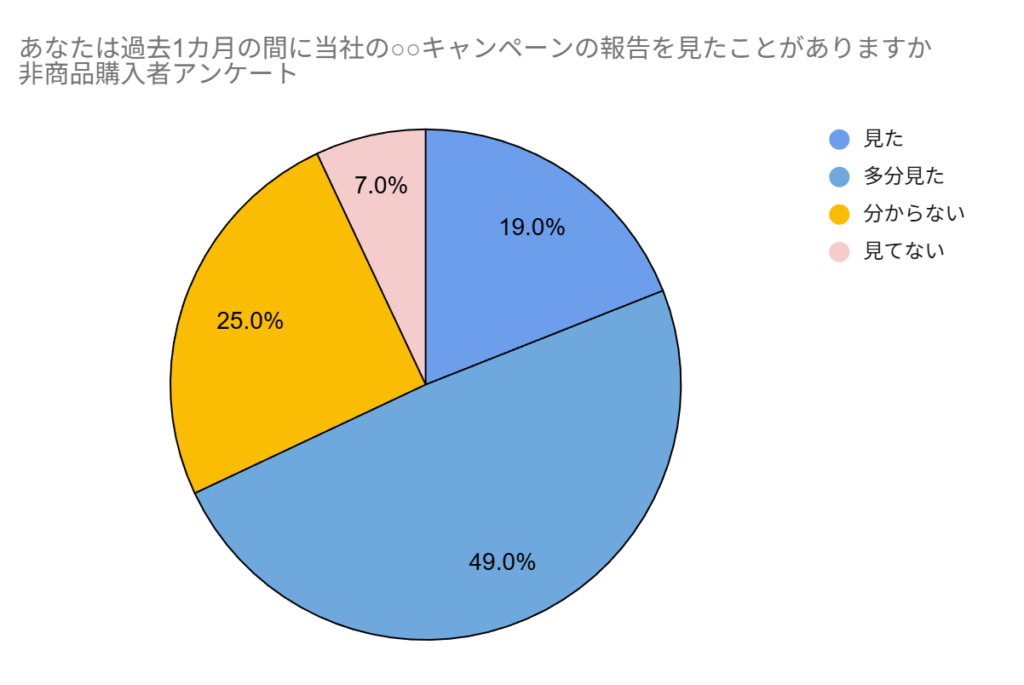
「7割が広告を見ているのに結局のところ購入に至ってない」これではむしろ、”広告を目にした人の方が商品を買っていない”ということになってしまいます。となると、”広告を見せたせいで買う気が失せるような内容が含まれていた可能性”を検討するべきだ。と著者は言います。
これは確かに、、、。むしろキャンペーン、失敗なのでは。。。
この後、さらに例を挙げてくれます。
ある食べ物を禁止するか検討します。
・心筋梗塞で死亡した日本人の95%以上がずっとこの食べ物を食べていた
・凶悪犯の70%が犯行前24時間以内に食べていた
・日本人はこれを食べることを禁止するとストレス状態が見られることがある
・江戸時代以降日本で起こった暴動のほとんどはこの食べ物が原因
答えは「ごはん」です。禁止にしても意味がなさそうですね。
このように、こんな単純集計だけ、こんな統計解析しかできないのであれば、意味がないのです。
しかし残念ながらこのような無意味な分析はこの世にあふれているとのこと。
ですが、「十分なデータ」をもとに「適切な比較」と行う統計的因果推論の基礎さえ身に着ければよいとのことです。
ちょっとの工夫で売り上げ60億円のアップ
なぜ自社商品を買ってくれて、なぜ買ってくれないかの違いが明らかにできれば、買ってくれる人を増やすことができるかもしれません。
例えば、広告を見たか否かの差により購買率が何十%と違うなら広告を増やした方がいいかもしれない、友人に紹介されたかの経験の有無の差なのであれば、既存客に対して友達紹介キャンペーンを展開してみてもいいかもしれない。
しかしこれらの差異は「経験と勘」と言ったものが多かったりする。
でも、この経験と勘は言い換えれば「あるある」になるわけですが(ちなみにIT業界にはたまによくあるという不思議なワードがあります)
この「あるある」の多くは「記憶の偏り」によって左右されるものと心理学者や認知科学者たちによって実証されています。この「記憶の偏り」はビジネスの成功法則もほんの数例程度の偏った成功体験を過剰に一般化してしまっているかもしれません。そして人間は誰しも一度先入観を持つと、全て都合よく解釈してしまう認知的な性質を持っています。統計学はそのような人間の欠陥を補うことができるそうです。
ここで著者が関わった小売企業がDMの送り方を変えただけで売り上げが60億UPした例があります。
データ分析をした結果最も大きな購買の差を生んでいるのは「DMを送られていたかどうか」だったそうです。今まではDMを無造作に送っていたそうです(会員100万人、年4回、延べ30万通のプレゼントキャンペーン付きDM、1通100円、3000万円のコストを使用していた)。年4回送付をしているので、3カ月ごとで期間を区切り分析した結果、DMを送られた人の売り上げとそうでなかった人の売り上げで500円分の売り上げの差異があり、DMを送りさえすれば500円の増加が見込まれる可能性が出てきました。この小売り企業は会員全員(+70万通)にDMを送り付けるということをするだけで20億円売り上がることが分かりました。
さらには「DMを送られることで売り上げが伸びる客層とそうでない客層の違い」や「顧客の売り上げを伸ばすDMと延ばさないDMの違い」など判別ルールを明らかにしたそうです。
そのルールに従ってDMを送り分けることで、DMの送付自体はほとんど変えなくても売り上げに6パーセント、60億円売り上がることができたのです。
実際に、クライアント企業はDMを送ると売り上げが伸びること、反応のいい顧客の特徴は経験としてそういえばそうだと一致していたそうです。
よって実際のデータを使い網羅的な比較を行うことで「なんとなく」ではなく、「今一番何をするべきか」という戦略目標が明らかにできるのです。
このような要因ごとの比較集計は「クロス集計」と呼ばれますが、著者は、これが統計学の力かというとそうではなく、これだけではまだ皮算用(物事がまだ実現しない前から、あれこれあてにして計算すること)に過ぎないと発しています。
これだけでも純粋に凄いと思いましたが、そうですか、今のところですと机上の空論なのですね。
まだまだ統計学の力はあるそうです。
誤差を見つめる、p値5%という希望
数学が苦手な方は数字とアルファベットや記号がセットで視界に入るとめまいがすると思いますが、安心してください。私もいきなりp値と言われて困惑してます。
「誤差を考えない試算は皮算用」と著者は言います。
先ほどの著者のクロス集計は誤差をまったく配慮していないものとなっています。
ここでフィッシャーという方が登場してくるのですが、
「フィッシャーたちの時代とそれ以前の統計学の大きな違いは誤差の取り扱いにある」と著者は言います。
先ほどナイチンゲールが登場しておりましたが、ナイチンゲールは1820年から1910年にかけて活躍し、フィッシャーは1890年から1962年と20世紀前半に統計学を発展させた人物です。
ナイチンゲールが活躍していた19世紀の統計学では、まず現状を可視化することが重要であり、誤差を厳密に評価しなくとも、結論が揺らがないほど明確な差を示すことが主な役割でした。
一方でフィッシャーらの時代になると、観測された差が偶然によるものかどうか、誤差が結果にどの程度影響しているのかに目が向けられ、「誤差を考慮したうえで意味のある結果かどうか」を判断するための統計学へと発展していきました。
先ほど「DMを送られた人の売り上げとそうでなかった人の売り上げで500円分の売り上げの差異があり、DMを送りさえすれば500円の増加が見込まれる可能性が出てきました。」と記載しましたが、この500円は単純な推定なので誤差が含まれており、場合によっては300円や1000円、ひどいときにはDMを送らない方が売り上げが高くなったり(どマイナス・・・)という可能性があるわけです。
最悪、誤差によって今回だけたまたまDMを送った人たちの平均売り上げが高かっただけだった。だったり、DMのコストを超えられない場合もあり得るのです。そうするとさっきの夢はあっという間に崩れますね。。。
このような誤差を考えない皮算用は他にもあるようです。
ちなみに皆さんは「A/Bテスト」ってご存じですか?
私はこれもIPAの試験で見た気がするんですよね、AとBの2パターン(複数パターンでもいい)を用意して比較検証するものです。
例えば、WEB画面を2種類用意してどちらがより会員になりやすいかとか、購入してくれるかなどをランダム表示して集計を取ったり、期間を区切って各パターンの集計を取ったりします。
そして優れたパターンが実際に採用されます。
ちなみにこの「A/Bテスト」のランダム表示して集計を取ることは「ランダム化比較実験」、期間を区切って各パターンの集計のようなランダムさが含まれずに集計を取ることは「準実験」と呼ぶそうです。
このテストがどこに関係してくるの?って話なのですが、著者の経験としてあるEC企業が積極的にA/Bテストを行っていたそうです。大きな企業なら0.1%すら億単位の売り上げになるわけですので、真剣になるわけです。今回のテストはAとBそれぞれ10万人をテスト対象としたそうです。
しかし、誤差を考えないと、これも水の泡になってしまいます。
こうしたクロス集計について意味のある偏りなのか、誤差でもこれくらいの差は生じるのか、と言ったことを確かめる解析手法にカイ二乗検定というものがあります。
実際には何の差もないのに誤差や偶然によってたまたまデータのような差(正確にはそれ以上に極端な差を含む)が乗じる確率のことを統計学の専門用語でp値と呼ぶそうです。
このp値が小さければ(慣例的には5%以下)それに基づいて科学者たちはこの結果は偶然得られたとは考えにくいと判断するそうです。
そしてそんな中、そのEC企業のA/Bテストのp値は44.7%・・・目も当てられません。
しかし、では0.1%の差に意味がないのかというとそうではなく、きちんと統計学的に立証できるサンプルサイズ今回ならそれぞれのパターンに100万人ずつのデータがあれば誤差は小さくなるのです。
どんなデータを解析したらいいのか
ここまでの説明の中で、「適切な比較を行うこと」と「誤差やp値まで含めて評価すること」の2点を意識すれば、経験と勘を超えられます。
(ちなみにシステム開発の見積もり手法にKKD法というものがあります。
勘(Kan)、経験(Keiken)、度胸(Dokyou)……改めてすごい方法ですね。)
よし分かった!データを分析してみよう!といざデータ分析を行う際、何と何を比較すればよいのか。が立ちはだかります。分析手法が分かっていても、どのようなデータを収集するかが重要になってきます。確かにそうですよね、数学の公式が分かっていても材料となる数字が間違えていたらそりゃ計算も狂い、本当に欲しかった計算結果が出てこないですからね。
著者は「目指すゴールを達成したもの」と「そうでないもの」の違いを比較さえすればいいと言います。
例えば、医療的な関係者なら「健康に長生きしている人」「早死にした人」
教育的な関係者なら「高い学習達成を示した子供」「そうでない子供」
心理学者で「幸福感の高い人」「そうでない人」で比較した方もいるそうです。
ビジネスにおけるゴールは、多くの場合「利益を上げること」です。
そのためには、需要を伸ばすか、コストを下げるか、その両方が必要になります。
本書ではCPU温度やメモリ使用状況などをモニタリングしたログをもとに「サーバーがダウンする状況」と「しない状況」と比較した結果、システムの増強と管理に割くコストを大幅に削減できたというケースがあるそうです。
重要なのは、「このデータで何か分からないかという漠然とした問い」ではなく、データのうち「何がどのような関係で利益と繋がっているか」だと言います。
因果関係には向きがあるらしい
因果関係とは、ある事象が別の事象を引き起こす「原因→結果」の関係を指します。
しかし、データを見ただけでは、その向きがA→Bなのか、B→Aなのか、分からないことが多いのです。
分かりやすい話題としては、子供が暴力的なテレビゲームで遊んでいたかどうかと子供の犯罪補導歴の有無の関連性を分析し、少年犯罪者の方が暴力的なテレビゲームで遊んでいる割合が高かったという結果が得られたとしても、暴力的なテレビゲームを規制して犯罪率が下げられるかどうかは良く分からないそうです。
もともと暴力性が高い子供がその手のゲームを好んだり、犯罪にも手を染めやすいと言った因果関係の可能性もあるわけです。
たばこが依存症にするのか、依存症気質の方が煙草に手を出しやすいのか。みたいな。
では結局統計学って役に立たないではないか。と言われるとそうではないらしく、既存データから何かしらの誤差を考えにくい偏りを発見すれば貴重な示唆に富む仮説になるそうです。
こうした有望な仮説を抽出するスピードと精度こそが現代における統計学の第一意義である。とのことです。
この仮説が単独で価値を生み出すかは分からないが、その仮説が本当に正しいかどうかを実際に検証してみることができ、かつどのような検証を行えばどれほどの精度で仮説が確かめられるか分かることも統計学の大きな役割の一つです。
では、先のデータから因果関係の向きが分からないということは、実はこの比較している集団が同じ条件ではない、フェアではないことが由来するそうです。
他の条件は全く同じだが、ピンポイントの部分だけ異なっているという集団同士を比較できれば理想的な比較になるそうです。
しかし、この他の条件が全く同じがなかなか難しい。
先の暴力的なゲームの例を挙げると、「ほかの条件は全く同じだが、暴力的なゲームのプレーの有無だけが異なっている」という条件が良いのですが、家庭環境、子供の心理的傾向などが異なる時点で他の条件が全く同じにはならないのです。
しかし、統計学では2つの解決方法があるそうです。
1:関連しそうな条件を考えうる限り継続的に追跡調査し、統計学的な手法を用いて、少なくとも測定された条件についてはフェアな比較を行う
2:解析ではなくそもそものデータのとり方の時点でフェアに条件をそろえる
教育学の分野ではしばしば一卵性双生児を集めて遺伝子の影響をそろえたうえで実験を行ったりするらしいです。しかし、そんなことをしなくてもフェアな条件で実験はできるそうです。
いやいや、双子で実験って本当にあるんですかね?そこにびっくりしました。もちろん著者はさらに続け
倫理的に最大限の注意を払いつつ、適切なやり方で実証実験を行えば、比較のフェアさは最大限担保することができるそうです。
誤差の重要性と正しい比較ができるのだろうか
日常で出会う分析は、分析と言っておきながらただ集計し比較しているだけなことが多いのかなと若干心配になりました。そして誤差って「たかが・されど」とは認識していましたが、それでも画期的または致命的な誤差だけを気にしておけばいいのだということが意外でした。
次回は第四章を自分なりにまとめてみようと思います。



コメント